Relationship Between Density And Temperature

Density

Densityis a measure of how much mass there is in a given volume or amount of space. The density of any substance is calculated by dividing the mass of the matter by the volume of the thing.

In Fig. 2.two, book is represented by boxes and individual particles of affair are represented by colored shapes.

Box A has five spheres.
Box B is the same size, and has the same volume every bit box A, but box B has x spheres.
Box C has the same mass as box A, with v spheres, but box C has a larger volume than boxes A and B.
Box D has the same book and number of light-green spheres equally role A, but also includes other types of matter than the rest of the boxes—red circles and bluish cubes.

Fig. two.2. The boxes and colored shapes in this figure demonstrate the effects of irresolute mass and volume on density.

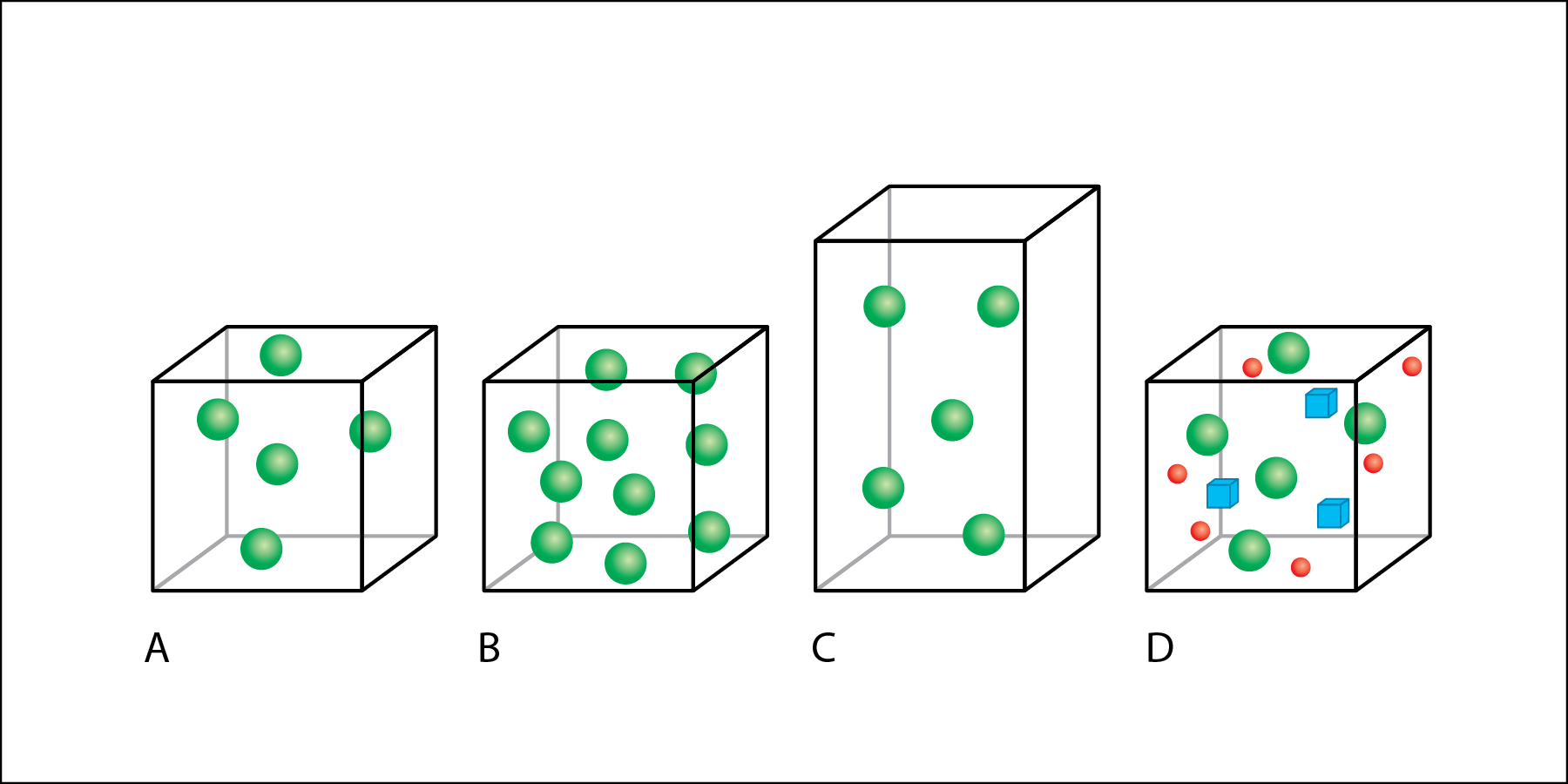
If the amount of matter is increased without changing the book, then the density increases (Fig. two.2 A to 2.ii B). If book increases without an increment in mass, and so the density decreases (Fig. 2.2 A to ii.2 C). Calculation additional matter to the same volume also increases density, fifty-fifty if the matter added is a unlike type of matter (Fig. 2.2 A to ii.two D).

Salinity Affects Density

When salt is dissolved in fresh water, the density of the water increases considering the mass of the h2o increases. This is represented by the improver of red spheres and blue cubes to the box from Fig. 2.2 A to Fig. 2.2 D. Salinity describes how much salt is dissolved in a sample of water. The more salt there is dissolved in the water, the greater its salinity. When comparison two samples of water with the same volume, the water sample with higher salinity will take greater mass, and it will therefore exist more than dumbo.

Temperature Affects Density

The density of h2o can too be afflicted by temperature. When the same amount of water is heated or cooled, its density changes. When the h2o is heated, it expands, increasing in volume. This is represented by the increment in the size of the box from Fig. 2.2 A to 2.2 C. The warmer the water, the more space information technology takes upwards, and the lower its density. When comparing two samples of water with the same salinity, or mass, the water sample with the higher temperature will have a greater volume, and information technology will therefore be less dense.

Relative Density

Fig. 2.3. (A) The pocketbook filled with yellow liquid is floating on the surface. (B) The pocketbook filled with orangish liquid is floating in mid-water (subsurface floating). (C) The bag filled with green liquid has sunk to the lesser of the beaker.

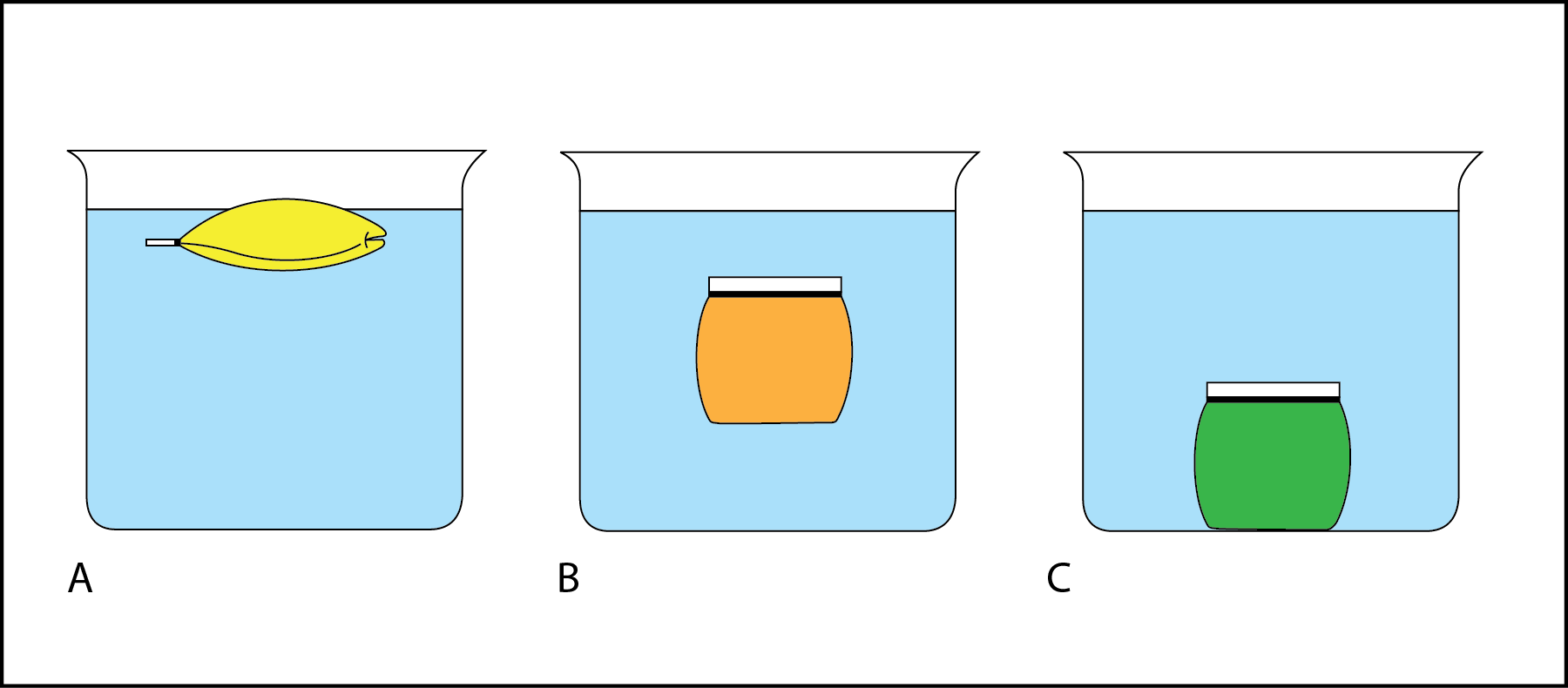
In Fig. 2.3, the beaker of liquid models a trunk of water like the bounding main or a lake. The bag of liquid simulates a layer of water. The relative density of the liquid in the bag compared to the liquid in the beaker tin be determined by observing whether the bag sinks or floats.

In Fig. two.3 A, the pocketbook rose to the elevation of the beaker and is now floating on the surface. The yellow liquid and the pocketbook are less dumbo than the liquid in the beaker.
In Fig. 2.3 B, the bag is floating in mid-h2o (subsurface floating). The orange liquid and the handbag are equal in density to the liquid in the beaker.
In Fig. 2.iii C, the purse sank to the bottom of the beaker. The green liquid and the bag are more dense than the liquid in the chalice.

Activity

Activity: Density Bags

Test the effects of salinity and temperature on the floating and sinking of liquid samples in numberless.

Water Layers

If h2o masses have salinity or temperature differences, they will grade h2o layers because they accept different densities. H2o layers can sometimes be felt when swimming. For example, on hot days the sun'southward heat can make water at the surface noticeably warmer than the deeper, cooler water. The relative density of 1 h2o mass in relation to another determines whether a layer of water floats or sinks.

Density and Buoyancy

Density tin be determined by measuring the mass and volume of an object. In the Density Bags Activity, density was not calculated. Instead, relative density was adamant by observing whether a bag of one liquid floated or sank in another liquid. A bag of liquid that sank was determined to be more dense than the liquid in the beaker. A bag of liquid that floated was adamant to be less dense than the liquid in the beaker.

Fig. ii.5. Forces on a red block in water. The buoyant force is represented past the letter
" title="

Epitome by Byron Inouye

The motion of any object is due to forces , which are pushes or pulls. Vertical—up-and-downwards—movement of water masses in the ocean can be explained in terms of two forces. The gravitational force (G) of the earth pulls downward and is proportional to the mass of an object. In Fig. two.five, the gravitational strength (G) is proportional to the mass of the red cake. The gravitational force on an object is also called weight . The strength due to gravity is greater on objects that are more massive, or weigh more. The buoyant forcefulness (B) of h2o pushes up. In the third century B.C., the Greek philosopher Archimedes was the starting time to describe buoyancy. He observed that the volume of water pushed out of a tub, or displaced, by an object was equal to the volume of the object. The buoyant forcefulness of the h2o is equal to the weight of the h2o displaced. This concept is known as Archimedes' Principle , and it explains why objects sink or float. In Fig. 2.5, the buoyant forcefulness (B) is equal to the weight of the water displaced by the blood-red block.

An object accelerates when the forces on that object are unequal. Although acceleration is unremarkably used to describe an object that is speeding up, the scientific definition of acceleration ways changing speed. An accelerating object tin can exist speeding up or slowing down. An object will always move in the direction of the greater strength. An object may accelerate downwards (sink) or upwards (rise) in a body of water.

Sinking is a downward vertical motility that occurs when the gravitational force (M) on an object is greater than the buoyant strength (B) supporting it (G > B).
Rising is the upward vertical movement that occurs when the gravitational force is less than the buoyant force (G < B).

If all of the forces on an object are counterbalanced, at that place is no acceleration. In this case, the object may non move—similar a volume sitting on a flat table—or the object may move at a constant speed—similar a car traveling at a steady 80 kilometers per 60 minutes. In the water, an object might remain yet either at the surface or within the water column.

Surface floating occurs when an object stays at the surface, considering the forces are counterbalanced at the surface (Yard = B).
Subsurface floating, or neutral buoyancy, occurs when an object maintains its position in mid-water, neither sinking nor rising (G = B).

Three cubes of the same size, but with different masses and thus different densities, are placed in iii beakers of water (Fig. 2.6). Because the cubes are identical in volume, they displace the same amount of h2o. By Archimedes' Principle, the buoyant forcefulness (B) interim on each cube is equal. Buoyant force is represented in Fig. 2.half dozen as upward pointing arrows, indicating the water is pushing up on the cubes. These arrows are the same length for each of the cubes, indicating that the strength of the buoyant strength acting on each cube is the aforementioned.

Considering the masses of the cubes are not equal, the gravitational force (G) acting on each cube is different. Gravitational force is represented in Fig. ii.6 as downward pointing arrows, indicating the gravitational forcefulness is pulling down on the cubes. These arrows are different lengths for each cube, indicating that the amount of the gravitational force is unlike for each cube. The downward pointing pointer in Fig. 2.vi A is the shortest, indicating that the yellow cube has the least mass and is the to the lowest degree dense. The downward pointing arrow is the longest in Fig 2.half dozen C, indicating that the green cube has the most mass and is the most dense.

The density of the cube relative to the density of water determines if the cube will float, sink, or be neutrally buoyant:

If the density of the cube is less than the density of the h2o, gravitational forcefulness will be less than the buoyant force (G < B), and the object will rise to the surface (Fig. 2.6 A).
If the density of the cube is equal to the density of the h2o, the cube will float in middle of the cavalcade of water considering the gravitational strength and buoyant force are balanced (G = B). This cube is neutrally buoyant (Fig. ii.6 B).
If the density of the cube is greater than the density of the water, the cube will sink considering the gravitational force is greater than the water's buoyant forcefulness (Chiliad > B) (Fig. two.half dozen C).